Benchmarking
Evaluation of Electromagnetic Software
Revised: June 4, 1997
© Copyright 1994, 1999 Sonnet Software, Inc. All Rights Reserved
Table of Contents
Chapter 1 - Introduction
Chapter 2 - Technical Overview
Chapter 3 - The Stripline Standard
Chapter 4 - The Stripline Standard and Triangular Subsections
Chapter 5 - The Microstrip Standard
Chapter 6 - The Coupled Microstrip Standard
Chapter 7 - Limit Tests
Chapter 8 - Lossy Ground Plane and Lossy Dielectric Tests
Chapter 5 - The Microstrip Standard
A Dispersion Primer | Benchmark Rational | Preliminary Microstrip Standard
The big advantage of the Stripline Standard is that an exact theoretical solution is available. The main difficulty is that it does not test dispersion. Thus, the focus of our recent research activities has been the development of a Microstrip Standard which allows precise characterization of error in the modeling of dispersion. The strength of microstrip as a standard is that it includes dispersion. The weakness, of course, is that there is no exact solution for microstrip. As is described in this chapter, we have a unique work-around for this problem.
Is this an "n-th decimal place", academic question? While dispersion in the velocity of propagation is well defined and understood, dispersion in characteristic impedance (Z0) sees a tremendous amount of controversy. Depending on which definitions are used and what techniques are used, calculated values of microstrip Z0 as a function of frequency can differ by over 20%! Keep in mind that a 5% error in either velocity of propagation or Z0, depending on the circuit, can reduce the probability of success on first fabrication to that of using only circuit theory design. An error of 20% virtually guarantees failure.
As of this writing, research on the microstrip standard is not complete. We shall, however, provide you with information on its current status. Research is sufficiently mature that we can provide a standard that will allow precise evaluation of error in the evaluation of dispersion. But first, a little intuitive explanation of dispersion and why it is a problem is appropriate.
A dispersive media is one in which the velocity of propagation or characteristic impedance change as a function of frequency. If a narrow pulse enters a dispersive transmission line, its different frequency components travel with different velocities. This causes the pulse to spread out, or become "dispersed" in time.
In a transmission line with uniform dielectric everywhere (e.g., coax, stripline, etc.) and no loss, we have TEM (Transverse Electric Magnetic) propagation. This means that there is no electric field and no magnetic field in the direction of propagation. If the transmission line goes along the Z axis, then EZ and HZ (or BZ) are zero. With no longitudinal fields there is no dispersion.
If we introduce loss, there must now be an electric field along the length of the line (EZ). This is exactly analogous to saying that when current flows through a resistor, there must be a voltage across (along) the resistor. This causes dispersion. In addition, the loss is usually frequency dependent. This also causes dispersion. The Microstrip Standard does not evaluate dispersion due to loss. All structures in this standard are lossless.
If we make the transmission line dielectric inhomogeneous (i.e., more than one kind of dielectric), EZ and HZ can no longer be zero and we have dispersion. Microstrip is an inhomogeneous media because some of the transmitted energy flows in the substrate and part in the air above the substrate.
At least for microstrip at low frequencies, EZ and HZ are very small and their effect is almost inconsequential. In this case we have Quasi-TEM propagation. It isn't really TEM but it acts a lot like TEM. At higher frequencies, dispersive effects can approach a 10% or more. In some cases, this is not important and error in evaluating dispersion is not a problem. In other cases, error in could representing dispersion seriously reduce the probability of success on first fabrication and thus must be accurately represented.
So what causes this kind of dispersion? An intuitive way to look at it is that a portion of the transmitted energy is in the substrate and a portion in the air above the substrate. As we increase frequency, the respective proportions change. This changes the velocity of propagation and Z0.
All models of microstrip dispersion agree that the velocity of propagation increases as frequency increases. However some models predict the same for Z0 while others predict that Z0 behaves non-monotonically, first decreasing then increasing.
We agree with the non-monotonic model and suggest the following intuitive description. At low frequency the current distribution across the width of the line remains unchanged but the electric fields surrounding the line slowly concentrate under the substrate as the frequency increases. This increases capacitance per unit length and decreases Z0 while increasing velocity of propagation. Then at a certain frequency (which is strongly dependent on sidewall and top cover distance), the current starts quickly concentrating on the edges, increasing the series inductance as frequency increases. This now dominates over the increasing capacitance causing the Z0 to start increasing. Velocity of propagation continues to increase.
We find the low frequency behavior of microstrip (before the series inductance starts changing) is only very slightly dispersive in Z0. In fact the decrease in Z0 is often so slight that it could be considered almost constant.
Since an exact theoretical solution for microstrip does not exist, we must attack the problem indirectly. Since we cannot simply compare an exact theoretical answer to the answer calculated by the analysis, we must look for some effect that Z0 has on a known component. This component then becomes our impedance standard.
Assume we have a lumped (small with respect to wavelength) element that we can place in a microstrip line. Assume also that we know the impedance of that lumped element exactly. Then we measure the element using a calibration algorithm which requires a transmission line of known characteristic impedance. If the characteristic impedance of that line is in error by, say, 10%, then the measured value of that lumped element is also in error by 10%. Thus the error in Z0 is equal to the error in the measured value of the lumped element.
The fundamental problem is that no matter what component we choose, there are fringing fields associated with that component. The fringing fields store inductive and capacitive energy, thus changing the apparent impedance of the impedance standard. If the fringing fields are uncontrolled, the so-called impedance standard is no longer a standard.
The key to creating an accurate microstrip impedance standard is to control the lumped element fringing field stray discontinuities, as shall be described in this section.
Note that this standard is focused on quantitative determination of only the error due to dispersion. Although it could easily be changed, this standard is intentionally insensitive to subsectioning error. Subsectioning error is treated in detail in previous chapters.
For the lumped "standard impedance" element, we select a capacitor connected in series in the center of a microstrip through line, see Figure 7. The capacitor dielectric extends across the entire substrate surface. Otherwise, this benchmark would be appropriate only for 3-D arbitrary analysis tools. The problem geometry, as given, is suitable for any 3-D planar tool which can handle two layers.
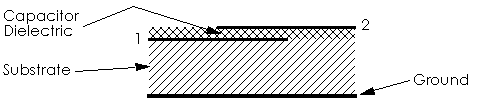Figure 7. Side view of the Microstrip Standard, a series (DC
blocking) capacitor. See text on control of fringing discontinuities.
Before we can use a series capacitor as a microstrip standard, we must first understand and control the fringing field discontinuities. There are two such discontinuities, shunt capacitance to ground and series inductance. The shunt capacitance to ground is almost entirely from the bottom plate of the capacitor. The top plate of the capacitor is shielded from ground by the bottom plate. Thus port 2, in Figure 7, has no capacitance to ground.
The series inductance is not so easily handled. That there is series inductance is easily understood. The current distribution across the width of the microstrip line is different from the current distribution across the width of the capacitor plate. When current flows from the line to the capacitor plate, transverse currents must flow in order to transition the current from that on the microstrip line to that on the capacitor plate. This transverse current is the series inductance, Figure 8.
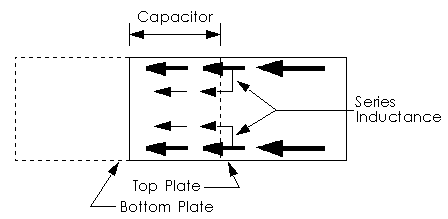Figure 8. Top view of the series capacitor showing conceptual
current flow. As the current distribution transitions from that on the microstrip line to
that on the capacitor, a transverse current must flow. This causes a series inductance.
With this understanding, we can do two things to counter the undesired effect of the series inductance. First, we can simply make the line width narrower. This makes the distance that the transverse currents flow shorter and the corresponding inductance smaller.
Second, we can make the capacitance smaller so that the capacitive reactance is much much larger than the inductive reactance. Effectively, both of these measures may be used to move the series LC resonant frequency up far above the desired measurement range leaving the frequency independent capacitor unchanged.
Note that whatever small effect is left from the series fringing inductance, it increases the apparent error by making the "frequency independent capacitor" appear to vary with frequency. Thus, the results of this benchmark should be treated as upper limits to the error of an analysis. The analysis could actually be better than results of this benchmark indicate to the degree that the series fringing inductance influences the capacitor.
Now we have one last assumption: The capacitor is frequency independent. This will be true if all the displacement current of the capacitor (i.e., electric field lines going from one plate to the other) all pass through material of the same dielectric constant and that dielectric constant is independent of frequency.
There is one more aspect of the geometry we can control to realize a good standard, substrate thickness. While we can move the series resonant frequency as high as possible, as described above, we can also move the dispersive frequencies as low as possible. This is done by making the substrate thick, effectively moving the dispersive frequencies much lower. While expensive to do in experimental work, it is just a few keystrokes on a computer.
Preliminary Microstrip Standard
We use the following dimensions for a microstrip standard which meets the above criteria for control of the fringing discontinuities:
| Line width: 0.5 mm. Capacitor size: 0.5 mm square. Substrate dielectric thickness: 10.0 mm. Substrate dielectric constant: 10.0. Capacitor dielectric thickness: 0.1 mm. Capacitor dielectric constant: 10.0. Reference planes: Placed at the center of the capacitor. Port-to-port distance (see text): 10.0 mm. Sidewall-to-sidewall distance (see text): 5.0 mm. Top cover distance (if present): Large (we used 1000 mm). Subsection size (see text): 0.25 x 0.25 mm. Loss: Completely lossless. Metal thickness: 0.0 mm. Frequency range: Multi-mode propagation starts at 10 GHz. Standard is not valid when higher order transmission line modes, box modes, surface waves, or radiation are excited. If sidewalls are not present, frequency range is degraded to under 5 GHz. Static, "correct capacitance", frequency: 0.1 GHz. |
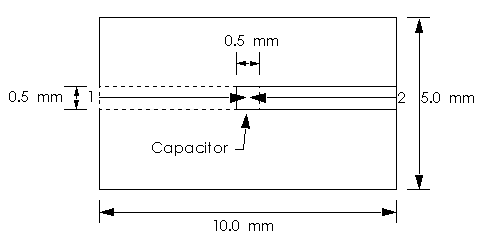Figure 9. A top view of the series capacitor. The port 2 line
on the right forms the top plate of the 0.5 x 0.5 mm capacitor. The port 1 line (dashed
lines) enters from the left with it's right end forming the capcitor's bottom plate. The
port 1 line is under the 0.1 mm thick capacitor dielectric.
The port-to-port distance (Figure 9) is the length of the through line into which the series capacitor is inserted. The length depends on the requirements of the analysis being evaluated. in the case of Sonnet, we recommend a transmission line of at least one substrate thickness in length between each port and the device under test. Requirements for other analyses may differ.
We found that a sidewall-to-sidewall distance of 5.0 mm increased the usable frequency range of this transmission line from 5 GHz to 10 GHz, as determined by the onset of multi-mode propagation. If sidewalls are not present, or if they are placed at greater distance, the microstrip standard can still be evaluated, however it is correspondingly limited in frequency range.
The subsection size selected allows the transmission line to be subsectioned two cells wide. Since the line is symmetric, this is the same as one cell wide. Based on our results with the Stripline Standard, we can expect that this generates numbers which are all about 5% in error due to the subsection size. However, as described below, the subsectioning error subtracts out leaving only dispersion error.
When analyzing the standard, it is simplest to look at the resulting Y-Parameters. In Sonnet, just use the -y command line analysis option. If Y-Parameters are not easily available, read the resulting S-Parameters into a circuit theory program and convert them to Y-Parameters. Then, since the top plate is connected to port 2, Y22 is just the admittance of the capacitor. If the capacitance is constant with frequency, Y22 should be linear with frequency.
To calculate "Dispersion Error", we take the capacitance at low frequency (in this case, 0.1 GHz, we also get the same answer at 0.1 MHz as a check), as calculated by the software. Even though this value of capacitance includes subsectioning error, we use it the "correct capacitance value" for the purposes of calculating Dispersion Error. Assuming that the subsectioning error is independent of frequency, this value of "correct capacitance" means that all subsectioning error subtracts out and we are left with nothing but dispersion error.
| Table 1: Sonnet Results For The Microstrip Standard | |||||
| Frequency (GHz) | Dispersion Error | Z0 (Ohms) | Percent Z0 Dispersion | eeff | Percent eeff Dispersion |
| 0.1 | 0.00% | 85.37 | 0.00% | 5.53 | 0.00% |
| 1.0 | 0.00% | 85.34 | - 0.04% | 5.54 | 0.18% |
| 2.0 | - 0.02% | 85.26 | - 0.13% | 5.55 | 0.36% |
| 3.0 | - 0.06% | 85.13 | - 0.28% | 5.58 | 0.90% |
| 4.0 | - 0.07% | 85.01 | - 0.42% | 5.63 | 1.81% |
| 5.0 | - 0.06% | 84.92 | - 0.53% | 5.68 | 2.71% |
| 6.0 | 0.02% | 84.94 | - 0.50% | 5.75 | 3.98% |
| 7.0 | 0.25% | 85.13 | - 0.28% | 5.82 | 5.24% |
| 8.0 | 0.77% | 85.55 | 0.21% | 5.89 | 6.51% |
| 9.0 | 1.02% | 85.79 | 0.49% | 5.94 | 7.41% |
| 10.0 | 7.12% | 78.41 | N/A | 5.66 | N/A |
The value of Y22 (normalized to 1/50 Mhos) for the Sonnet analysis at 0.1 MHz is 9.321 x 10-6. Each analysis tested with this standard should generate a different "correct capacitance" value. The differences are due to differences in subsectioning error. Comparing these low frequency differences between analyses can be interesting, but it is not the intention of this standard. Rather, we are interested in how accurately dispersion is represented and thus we must look at how each analysis result changes with respect to its own "correct capacitance" value as we increase frequency.
The Sonnet results for the Microstrip Standard are shown above. The column labeled "Dispersion Error" is the key result of the Microstrip Standard. It forms an upper limit to the error in the analysis due to dispersion. For this transmission line geometry, dispersion error starts increasing at 7 GHz, becoming large at 10 GHz. At 10 GHz, Z0 takes a sudden large decrease indicating the onset of multi-mode propagation, thus the results are no longer valid ("N/A").
When applying these results to different transmission line geometries, the frequencies should be scaled according to the onset of the first higher order propagating modes, which happens for this line at 10 GHz. Thus, we can view the result at 7 GHz to be at 70% of the upper frequency limit for this line. We can expect similar dispersion error for other microstrip transmission lines at 70% of their upper frequency limit.
The remaining columns are informational, providing what Sonnet calculates for characteristic impedance and effective dielectric constant. This is useful to see how strong dispersion is. We can be confident that these numbers are at least as accurate (ignoring subsectioning error) as indicated in the dispersion error column because any error in the calculation of dispersion causes the capacitance to appear to change as a function of frequency and this translates directly into error in the dispersion error column.
Notice the non-monotonic behavior of Z0. All Z0 dispersion (except 10 GHz) is less than about 0.5% as calculated by Sonnet. If an analysis were to predict large values of dispersion for this structure, it is dramatically seen in the dispersion error. Thus, to within a percent or so, the Z0 of this line can be treated as dispersionless. If the line is incorrectly treated as having a strong Z0 dispersion, the probability of success on first fabrication can be severely compromised.
In contrast, the effective dielectric constant sees strong dispersion.
