Sonnet Suites - Beowulf
Sonnet is excited to preview our upcoming fast solver, Beowulf. The first round of beta testing is now complete. Based on what we learned, we'll be deploying a second beta open to all on-maintenance HPS customers. Upon release--bundled with the production v19, scheduled for May 30 2025--all Sonnet customers with current software maintenance agreements on HPS license may download, install and license this powerful new release upon request. The software will be available by download from Sonnet's web site, and customers are invited to contact their Sonnet Technical Sales Representative for details on accessing the release download.
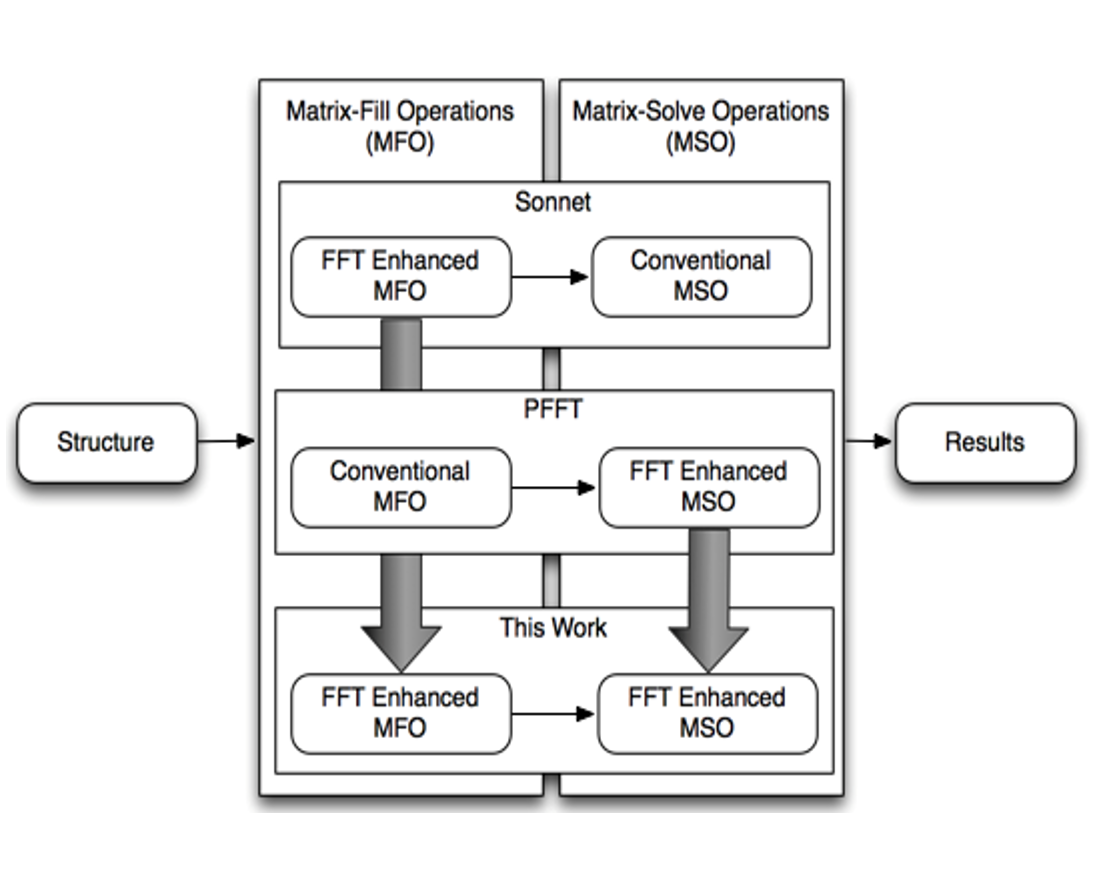
The Unified-FFT Method
Beowulf will be the first commercial tool to leverage the award-winning Unified-FFT (UFFT) method, which scales as O(N log N) without sacrificing accuracy or precision. Developed at Syracuse University in 2014, Unified-FFT is an iterative method which leverages FFTs for both matrix fill and matrix solve. It utilizes an implicit matrix which leverages lossless compression, via redefining the moment matrix as a series of Toeplitz and Hankel arrays.
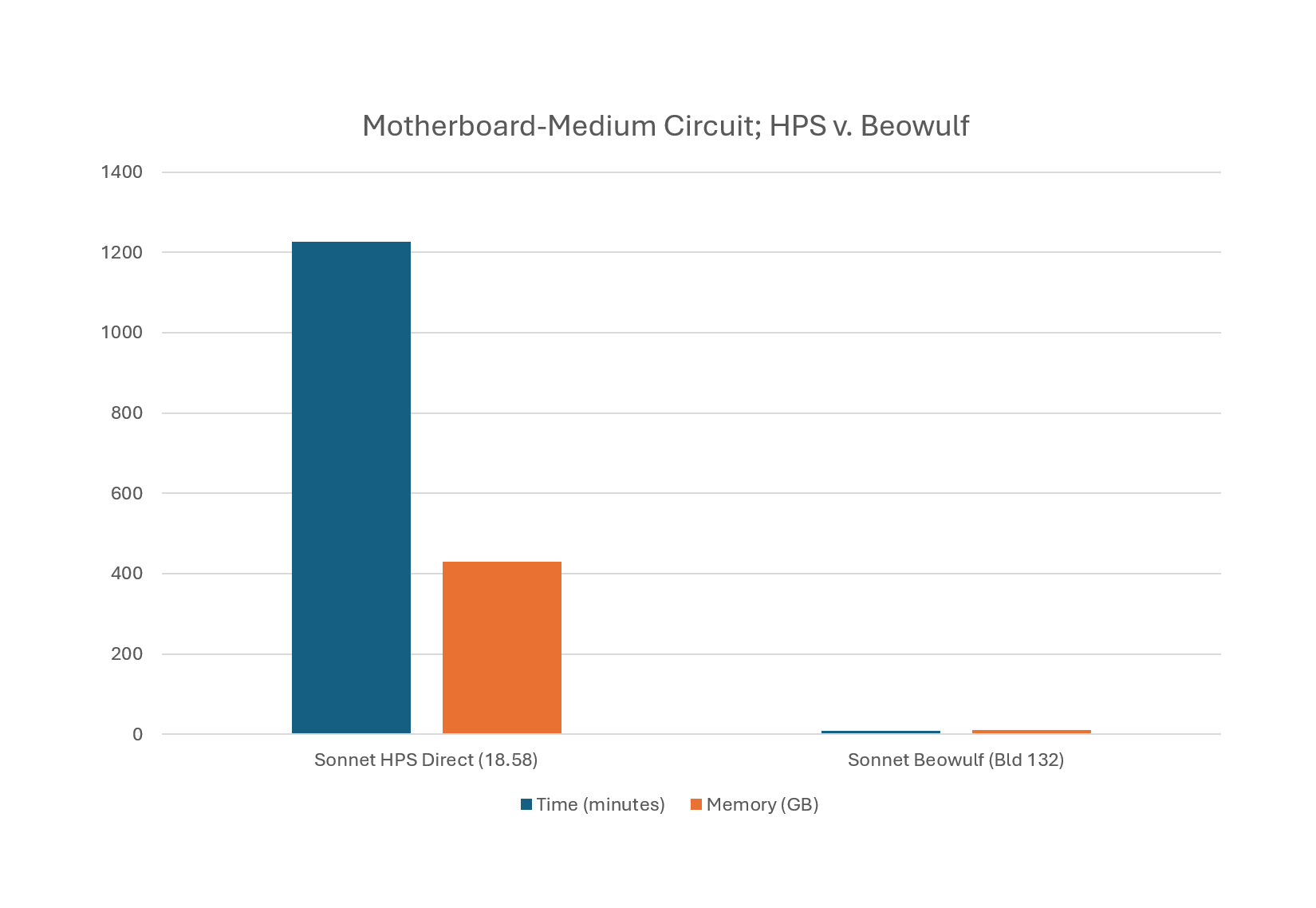
Extreme Speed, Reduced Memory
As no full-matrix factorization is necessary, the O(n log n) scaling allows Beowulf to run large circuits much faster. For large, well-conditioned problems, this can be orders of magnitude improvement. All while taking less memory to simulate due to the lossless compression.
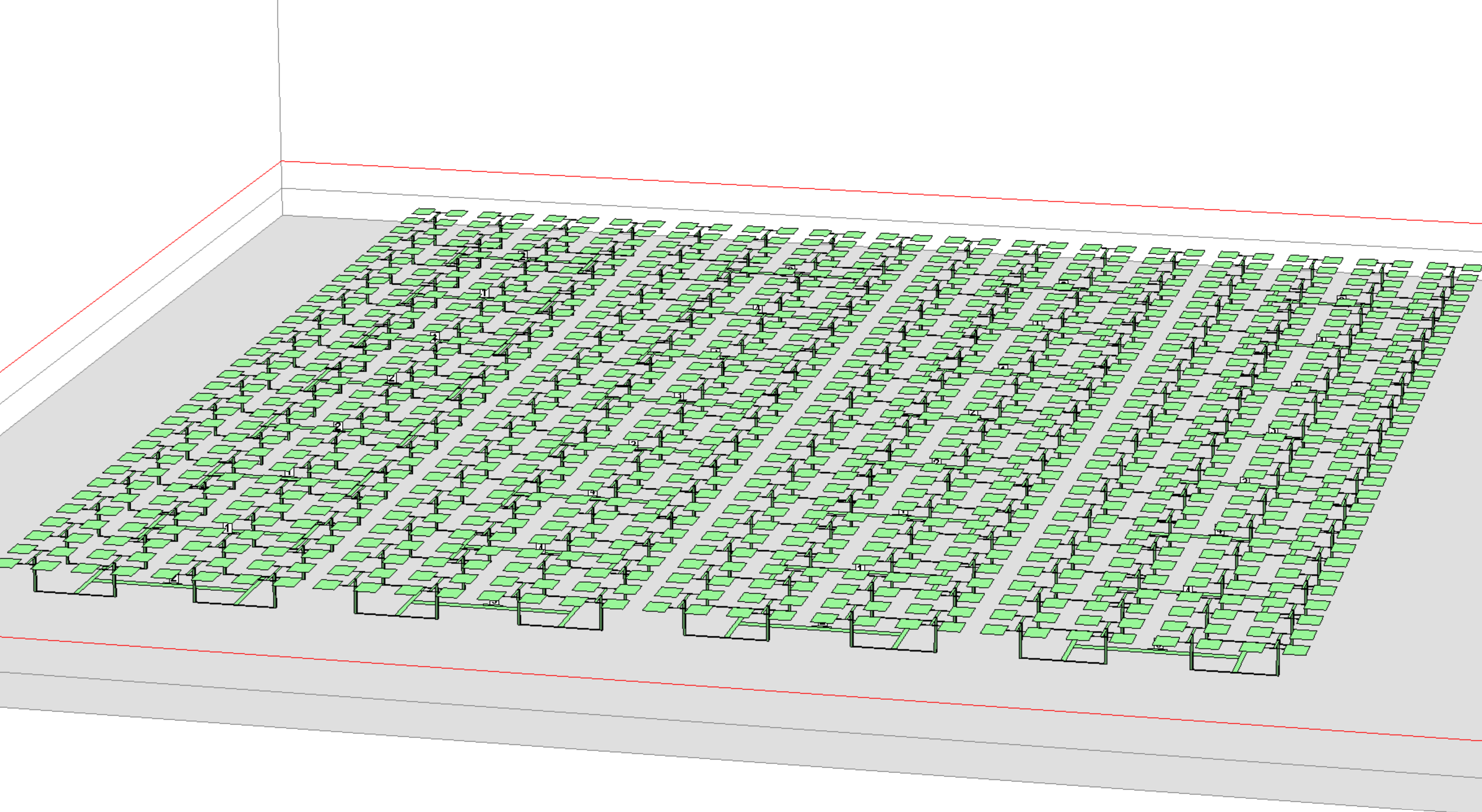
Solve Huge Problems without Huge Server Rooms
With the efficiency of Sonnet's 3D Planar framework combined with the UFFT method, Beowulf can solve tremendously large EM problems on relatively modest hardware. This 1,024 element patch antenna array was solved on a miniITX Intel Desktop system.
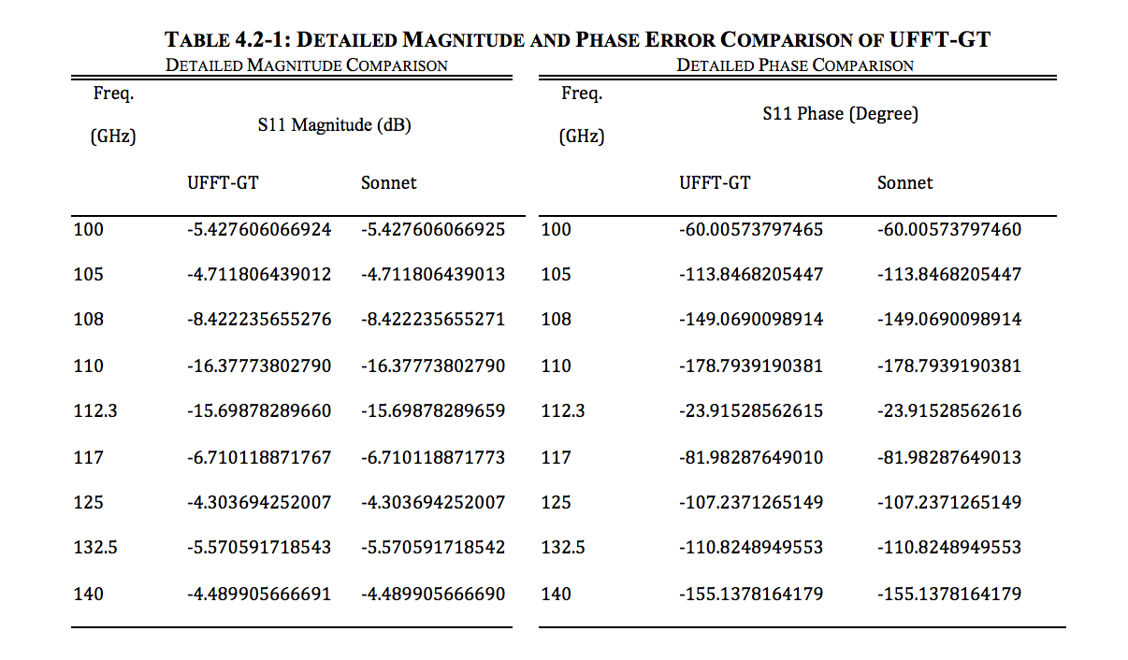
Unmatched Precision and Accuracy in a Fast Solver
When driven to it's full potential, Beowulf has been scientifically proven to provide the same accuracy and precision as Sonnet's world-renowned direct solver.
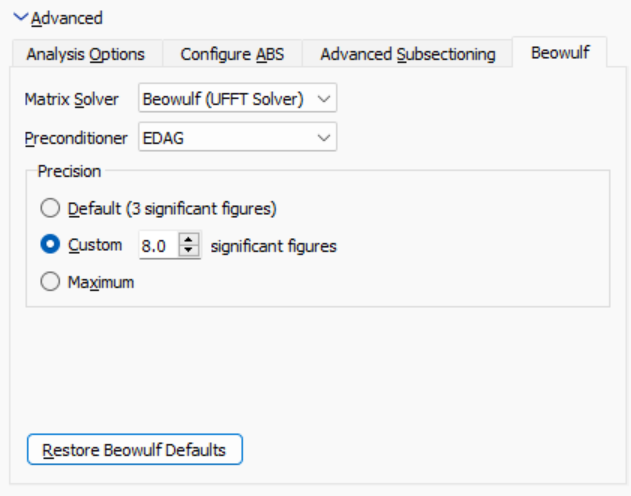
Selectable Performance/Precision
Beowulf allows you to define precisely how many significant figures you want in your simulation. Fewer gives you a faster simulation, more gives you more confidence in your results. You can go up all the way to 12 figures, which is a simulation residue of 0.0000000000001. Yes, really, FFTs on Toeplitz/Hankel arrays are effectively lossless.



