Analyzing circuits which have non-rectangular polygons can require extensive memory and processing time since the number of subsections needed to model the non-rectangular shapes is significantly higher than the number of subsections required for a rectangular polygon. Conformal meshing is a technique which can dramatically reduce the memory and time required for analysis of a circuit with diagonal or curved polygon edges.
This technique groups together strings of cells following diagonal and curved metal contours. Whereas staircase fill results in numerous small X- and Y-directed subsections, conformal mesh results in a few long conformal subsections. Fewer subsections yields faster processing times with lower memory requirements for your analysis.
In older meshing techniques, large non-rectangular subsections did not include the high concentration of current on the edge of the lines required by Maxwell’s equations. The results could significantly under-estimate loss and inductance. In contrast, the Sonnet conformal meshing automatically includes the high edge current in each conformal section. In conformal meshing, Sonnet can achieve the speed of using large subsections, and at the same time enjoy the accuracy of using small cells. This patented1 Sonnet capability is unique.
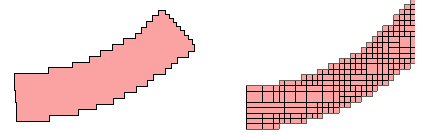
Conformal sections, like standard subsections, are comprised of cells, so that the actual metalization still shows a “jagged” edge when the polygon has a smooth edge, as pictured below. However, the sections can be much larger due to conformal meshing. You may now make the underlying grid sufficiently small to accurately resolve challenging circuit dimensions without incurring excessive memory and analysis time requirements.
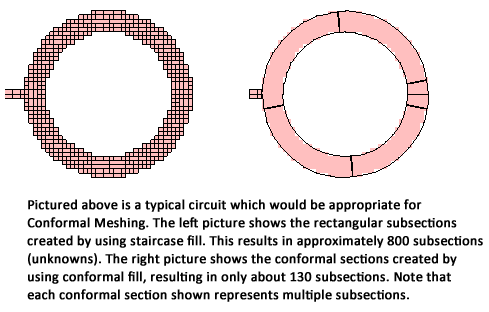
Conformal meshing should be used in places where it will reduce subsection count. For rectangular polygons with no diagonal or curved edges, it is more efficient to use rectangular subsections (default). However, if a polygon contains a curved edge, conformal meshing provides a quicker analysis.
For a discussion on subsectioning when using Conformal Mesh, see Conformal Mesh Subsectioning.
1 U.S. Patent No. 6,163,762 issued December 19, 2000.
Conformal meshing assumes most of the current is flowing parallel to the edge of the conformal subsection. This works well for transmission lines. However, this is usually not accurate for geometries like patch antennas and ground planes. For large areas of metal in both x and y directions, high current can flow parallel to the X axis edges, and parallel to the Y-axis edges at the same time. Conformal meshing can include only one of these currents. Thus, conformal meshing should only be used for transmission line geometries, which have a “line width” that is small compared to a wavelength.