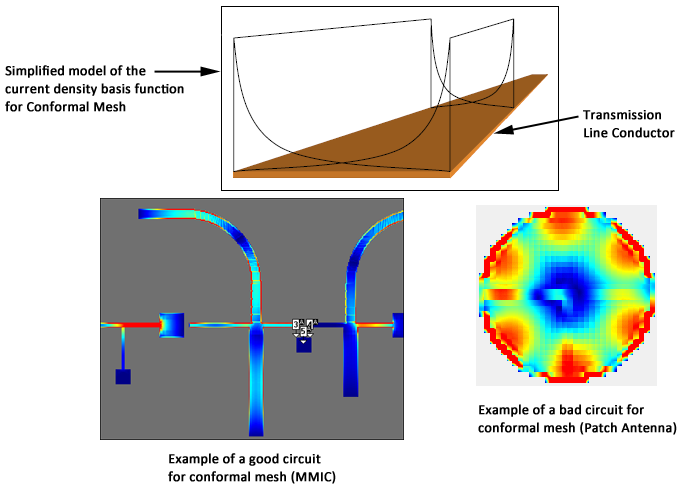
Conformal meshing is a technique which can dramatically reduce the memory and time required for analysis of a circuit with diagonal or curved polygon edges. Only the effect of conformal mesh on subsectioning is discussed in this chapter. Conformal mesh assumes that most current flows on the edges of circuit conductors, as shown below, and should only be applied when this holds true.
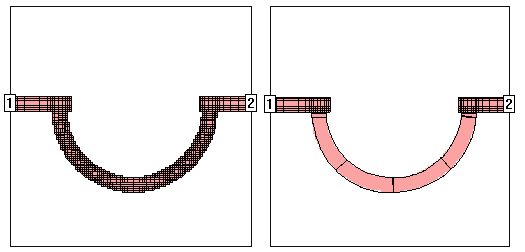
This technique groups together strings of cells following diagonal and curved metal contours to form long subsections along those contours. Whereas staircase fill results in numerous small X- and Y-directed subsections, conformal mesh results in a few long conformal subsections. The illustration below shows the actual metalization of a conformal section in close up alongside the same section using staircase fill.

Conformal sections, like standard subsections, are comprised of cells, so that the actual metalization still shows a ''jagged'' edge when the polygon has a smooth edge. However, the sections can be much larger due to conformal meshing. These larger sections yield faster processing times with lower memory requirements for your analysis.
Standard subsectioning requires a lot of subsections to model the correct current distribution across the width of the line. Conformal subsections have this distribution built into the subsection. Sonnet conformal meshing automatically includes the high edge current in each conformal section. This patented Sonnet capability is unique. (U.S. Patent No. 6,163,762 issued December 19, 2000.)
An example of a circuit using both standard subsectioning and conformal mesh is shown below. The circuit shown at the left is displayed using standard subsectioning (staircase fill). Conformal meshing for the curved part of the circuit is shown on the right. Note that for the curved part of the geometry, conformal mesh uses substantially fewer subsections than the number used in the standard subsectioning.