Most functions and operators should always use lower case characters. Use parentheses in your equation to delineate the order in which the operations should be performed. For example
((x * y)^2)
would multiply the complex number x by the complex number y and square the resulting complex number.
Entry |
Definition |
x + y |
Complex addition of x and y |
x - y |
Complex subtraction of y from x |
x*y |
Complex multiplication of x and y |
x/y |
Complex division of of x by y |
x^y |
Power x^y = x raised to the power of y |
Entry |
Definition |
db10(x) |
dB of a Power value (i.e. S21^2) = 10Log10(|x|) |
db20(x) |
dB of a voltage value (i.e. S21) = 20Log10(|x|) |
log10(x) |
The base 10 logarithm of the magnitude of x |
ln(x) |
The natural logarithm of the magnitude of x |
exp(x) |
Natural antilogarithm of x |
Entry |
Definition |
real(x) |
Real part of complex value x |
imag(x) |
Imaginary part of complex value x |
mag(x), abs(x) |
Magnitude of complex value x |
deg(x) |
Phase of complex value x in degrees |
rad(x) |
Phase of complex value x in radians |
cmplx(x,y) |
Complex: form a complex number from two values CMPLX(x,y) = ( x+iy) Note that this is the only way you can form a complex number. |
hypot(x,y) |
Euclidean distance between x and y |
conj(x) |
Conjugate of a complex number (( x+iy) -> ( x+iY)) |
Entry |
Definition |
sin(x) |
Sine of complex value x in radians |
cos(x) |
Cosine of complex value x in radians |
tan(x) |
Tangent of x with x in radians |
asin(x) |
Inverse sine of x with result in radians |
acos(x) |
Inverse cosine of x with result in radians |
atan(x) |
Inverse tangent of x with result in radians |
atan2(y,x) |
Inverse tangent of y/x with result in correct quadrant |
sinh(x) |
Hyperbolic sine of x with x in radians |
cosh(x) |
Hyperbolic cosine of x with x in radians |
tanh(x) |
Hyperbolic tangent of x with x in radians |
asinh(x) |
Inverse hyperbolic sine of x with result in radians |
acosh(x) |
Inverse hyperbolic cosine of x with result in radians |
atanh(x) |
Inverse hyperbolic tangent of x with result in radians |
Entry |
Definition |
fmod(x,y) |
Floating point remainder of x divided by y |
int(x) |
Truncated integral value of x |
max(x,y) |
Maximum of x and y |
min(x,y) |
Minimum of x and y |
sqrt(x) |
Square root of x |
Entry |
Definition |
m2p(x) |
Converts x meters to the present project units. For example, if project units are set to mils, it converts x meters to the equivalent number of mils |
h2p(x) |
Converts x Hz to the present project units. For example, if project units are set to GHz, it converts x Hz to the equivalent number of GHz |
p2m(x) |
Converts x project units to meters. For example, if project units are set to mils, it converts x mils to the equivalent number of meters |
p2h(x) |
Converts x project units to Hz. For example, if project units are GHz, it converts x GHz to the equivalent number of Hz |
When you graph the response of a circuit after completing a simulation, you may choose how to plot complex data (typically s-parameters) on the graph by using the Format droplist in the Manage Curves dialog box. This Format droplist gives you the following choices: Magnitude (dB), Magnitude, Phase (Deg), Phase (Rad), REal, and Imaginary. The FORMAT() function maps your choice from the Format droplist in the Manage Curves dialog box to your equation. For example, if you choose Real in the Format droplist of Manage Curves, then FORMAT(Z) will give you the real part of argument Z in your equation.
There are two additional functions that may be used in the project editor.
table1(" filename.csv", <key>) This function allows you to access values in a . csv file; saving a file from Microsoft Excel for example. Note that a comma must separate the two values. Note that the quote marks are required as part of the syntax.
" filename.csv" is the path of the . csv file you wish to access. If only the file name is specified (with no path), then the file should be in the same directory as the source project. You may use relative paths. <key> is the value from the first column of the desired entry in the . csv file. The function returns the second value. If the <key> value does not occur in the file, then linear interpolation of the file is used to return a value. Note that you may not extrapolate; the <key> value must fall between two existing values in the table. The key value does not have to be a fixed number; you may use the constant FREQ as the key or a variable. For example, you could define a variable as table1("example.csv", FREQ) which would define a variable which changes with the frequency according to the numbers in the table example.csv. Please note that the frequency units are in Hz. Comments should be preceded by an exclamation point (!). The exclamation point may be the first character in an entry or occur later in a line entry.
For example, you have the . csv file " example.csv" which contains the following entries :
! Project galaxy data
1,45
3,135
7,315 !My comment
8,360
then,
table1(" example.csv", 3) = 135
table1(" example.csv", 4) = 180
table1(" example.csv", 8) = 360
table2("filename.csv", <rowkey>, <colkey>) This function allows you to access values in a .csv file; saving a file from Microsoft Excel for example. Note that commas must separate the three values. While the table1 function allows you to have only one value per key, the table2 function allows you to define a row of multiple values, and use the two keys to identify a specific value in the row.
"filename.csv" is the path of the .csv file you wish to access. If only the file name is specified (with no path), then the file should be in the same directory as the source project. You may use relative paths. <rowkey> is the row number from which you wish to obtain a value and <colkey> identifies the column from which you wish to obtain the value. The function returns the value from that column in that row of the source file. If the <rowkey> or <colkey> does not occur in the file, then interpolation of the file is used to return a value. The key values do not have to be fixed numbers; you may use the constant FREQ or a variable as key values. Comments should be preceded by an exclamation point (!). The exclamation point may be the first character in an entry or occur later in a line entry.
For example, you have the .csv file "table2d.csv" which contains the following entries:
! Project galaxy data
, 1, 2, 3, 4, 5, 6
2, 2, 4, 6, 9, 10, 12
4, 4, 8,12,16, 20, 24
6, 6,12,18,24, 30, 36
8, 8,16,24,32, 40, 48
10,10,20,30,40, 50, 60
12,12,24,36,48, 60, 72 !My comment
14,14,28,42,56, 70, 84
16,16,32,48,64, 80, 96
18,18,36,54,72, 90,108
20,20,40,60,80,100,120
22,22,44,66,88,110,132
Line 1 is the list of column keys. All other lines are <rowkey> followed by the values in each column. Note that there is no value in the first position in the first line. This is an "empty" slot as it is the intersection of the row and column keys. The .csv file is displayed below in Excel to more clearly illustrate the format.
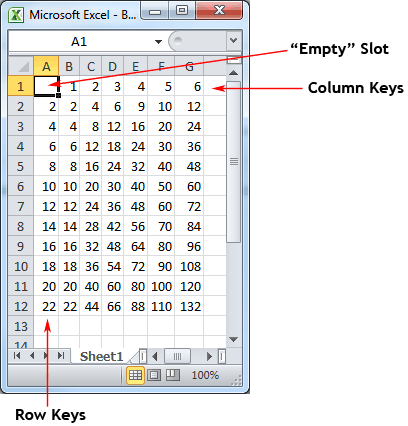
Then,
table2("table2d.csv", 2,4) = 9
table2("table2d.csv", 8,1) = 8
table2("table2d.csv", 16,3) = 48
table2("table2d.csv", 15.2,3.5) = 53.2
Note the comma at the beginning of the first line. It is not required by Sonnet, but if that comma is not present Excel will not parse the file. On the other hand Excel allows a dummy value before that first comma which is not accepted by Sonnet. Extra spaces are permitted.