Rdc/Rrf Loss Model

This method allows you to enter two values: RDC and RRF. The first parameter, RDC, determines loss at low frequency (where the conductor is much thinner than the skin depth). Surprisingly, other electromagnetic analyses often predict zero loss at low frequency because they assume RDC is zero.

The second parameter is the skin effect coefficient, RRF. Em multiplies this number by the square root of the frequency (in Hertz) to yield the Ohms/square value at high frequency.

The equations for RDC and RRF are:

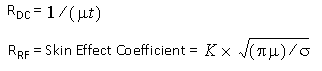
where:

σ: Bulk conductivity in Siemens/meter

t: Metalization thickness in meters

μ=μ0 x μr

μr = relative permeability of your metal, which is typically 1.0 for most metal materials. Magnetic materials, such as nickel, have a μr greater than 1 and therefore significantly decrease the skin depth.

K: A value between 0.5 and 1.0 and depends on the current ratio. For a detailed discussion of current ratio see Current Ratio. Shown below is a table of K values for typical applications:

Typical values for RDC and RRF are 0.004 and 3e‑7. If you start getting very strange loss results, check RRF, paying special attention to the exponent.

 Use this planar metal type if you wish to include the μr effects in the metal type. Sonnet allows you to do this by adjusting the RRF value.

Em also properly models the transition between electrically thin (low frequency) and electrically thick (high frequency) conductors. The transition frequency from RDC to RRF is the square of RDC/RRF. At this frequency, and a relatively narrow band around it, both coefficients are important. If the skin effect coefficient (RRF) is set to 0.0, then the value of RDC is used over all frequencies. This is the usual case for resistors.

The above equation for RRF assumes that all of the current travels on just one side of the conductor. This is a good approximation for some microstrip circuits. However, if the current really travels on both sides, this gives a pessimistic value for the loss. The equation should be modified for other structures. Stripline, for example, has current of equal amplitude on both the top and bottom of the conductor. In this case, you should divide the RRF value by two, while maintaining RDC.

As an example, the conductivity (σ) for copper is 5.8E+7 Siemens/m, giving RDC = 0.006 Ohms/square (t = 3 mm) and a microstrip RRF = 2.6E-7. In reality, the bulk conductivity of copper, or any other given metal, may not equal the laboratory value, so the figures as calculated above are likely to be lower than actual results.